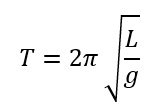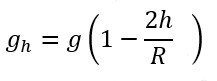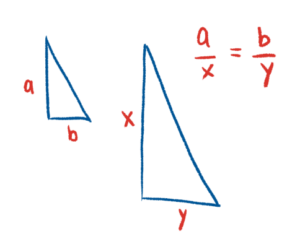เรื่องและภาพโดย วริศา ใจดี
ลองจินตนาการหากนักเรียนคนหนึ่งเปิดข้อสอบขึ้นมาและเจอคำถาม
“จงแสดงวิธีการวัดความสูงของตึกระฟ้าโดยใช้บารอมิเตอร์”
พร้อมเว้นที่ว่างหนึ่งหน้ากระดาษเต็มไว้ให้เขียนคำตอบ
ก่อนอื่นมาทำความรู้จักบารอมิเตอร์ หรือเครื่องตรวจวัดความดันอากาศกันก่อน
เครื่องวัดนี้ใช้หลักการการขยายหรือหดตัวของโลหะ หรือการเปลี่ยนระดับความสูงของปรอท เนื่องจากความดันอากาศภายนอก ซึ่งค่าความดันอากาศนี้เปลี่ยนแปลงไปโดย ขึ้นอยู่กับปัจจัยหลักคือความสูงจากระดับน้ำทะเล ยิ่งสูง ความดันอากาศก็ยิ่งต่ำ เพราะความหนาแน่นของโมเลกุลอากาศที่สูงมีน้อยกว่าที่ต่ำ ทั้งนี้ก็เพราะมีแรงโน้มถ่วงของโลก ดึงดูดโมเลกุลอากาศไว้ใกล้กับผิวโลก เมื่อสูงขึ้นไปจึงค่อยๆ เบาบางลง

ความดันอากาศ ณ ระดับความสูงต่างกัน
นี่เป็นกุญแจสำคัญที่ทำให้เราสามารถใช้บารอมิเตอร์หาค่าระดับความสูง (altitude) ได้จากความสัมพันธ์ระหว่างความดันอากาศกับความสูงจากผิวโลก
คราวนี้กลับมาที่ข้อสอบ หากนักเรียนคนนั้นจำหลักการข้างต้นได้ ก็จะสามารถเขียนคำตอบได้ว่า
“ใช้บารอมิเตอร์วัดความดันอากาศที่พื้น และที่ยอดตึก นำมาเทียบหาผลต่าง และแทนค่าเข้าไปเพื่อคำนวณผลต่างระดับความสูงในสูตร P=ρgh
เมื่อ ρ คือค่าคงที่ของความหนาแน่นอากาศ และ g คือความเร่งเนื่องจากแรงโน้มถ่วงของโลก มีค่าเท่ากับ 9.81 ms-2 หลังการแทนค่าและแก้สมการดังรูป ผลค่า h2– h1 ที่ได้ก็คือ ระยะจากพื้นถึงยอดตึก หรือก็คือความสูงของตึกตามที่โจทย์ถามนั่นเอง”

การคำนวณหาความสูง โดยใช้ผลต่างของความดันอากาศที่พื้นกับที่ยอดตึก
แน่นอนว่านี่คือคำตอบที่ถูกต้องสำหรับคะแนน 10 เต็ม 10 ถ้าจำได้ก็ทำได้ ยินดีด้วย ! คุณสอบผ่าน !
แต่ถ้าจำไม่ได้ขึ้นมา ก็คงจะต้องส่งกระดาษคำตอบเปล่าอย่างน่าเสียดาย
สำหรับการสอบเพื่อวัดระดับความรู้ความเข้าใจของนักเรียน ผู้ออกข้อสอบย่อมอ้างอิงข้อมูลจากตำราเรียนตามวัตถุประสงค์ชองหลักสูตรการเรียนการสอน คำตอบที่จะได้คะแนนเต็มอย่างง่ายดายโดยไม่มีข้อสงสัยจึงมีเพียงคำตอบเดียวและวิธีเดียวเท่านั้น
แน่นอนว่าคอลัมน์สาระวิทย์ในศิลป์วันนี้ไม่ได้มาสอนการคำนวณทางฟิสิกส์ แต่จะชวนมาดูเรื่องราวสุดฮิตของความแปลกในคำตอบของนักเรียนคนหนึ่ง กับการใช้บารอมิเตอร์ให้เกิดประโยชน์มากกว่าแค่วัดความดันบรรยากาศ เพราะสามารถคิดค้นวิธีการในการใช้บารอมิเตอร์หาความสูงของตึกได้อย่างหลากหลาย !
หลายคนอาจจะเคยได้ยินเรื่องนี้มาก่อน โดยเฉพาะเวอร์ชันที่เล่าว่า เป็นข้อสอบของมหาวิทยาลัยโคเปนเฮเกน ที่มี นีลส์ โบร์ (Neils Bohr) นักวิทยาศาสตร์รางวัลโนเบลสาขาฟิสิกส์ เป็นนักเรียนเจ้าของความคิดอันสวนทางกับผู้ออกข้อสอบ
จริงๆ แล้วต้นกำเนิดของปัญหาชวนคิดนี้มีที่มาจาก คุณอเล็กซานเดอร์ คาลานดรา (Alexander Calandra) นักวิทยาศาสตร์, นักศึกษาศาสตร์ และนักเขียน ผู้ได้รับการจดจำจากผลงานเรื่องสั้น “Angels on a Pin (101 Ways to Use a Barometer)” เผยแพร่ลงหนังสือพิมพ์ลอนดอนชื่อ Saturday Review ซึ่งก็คือสิ่งที่เราจะมาพูดถึงกันในวันนี้
เริ่มต้นจากนักเรียนคนหนึ่งที่ได้ศูนย์คะแนนในข้อสอบวิชาฟิสิกส์จากคำถาม “จงแสดงวิธีการวัดความสูงของตึกระฟ้าโดยใช้บารอมิเตอร์” เพียงเพราะว่านักเรียนคนนี้ ไม่ได้ตอบคำถามตรงตามหลักการในตำราที่เราได้เรียนรู้กันมา ดังวิธีที่ฉันแสดงให้ดูข้างต้น
หากแต่เขามีวิธีหาคำตอบที่พลิกแพลงกว่านั้น และแน่นอนว่าเขาไม่ยอมรับศูนย์คะแนนจากกรรมการตรวจข้อสอบที่บอกว่าคำตอบของเขานั้นผิดทั้งหมด
หลังจากกรรมการตรวจข้อสอบได้พูดคุยกับนักเรียนคนนี้อยู่นาน ก็พบกับคำตอบที่สร้างสรรค์แหวกแนวยิ่งขึ้นไปเรื่อยๆ
เริ่มตั้งแต่วิธีแรก วิธีที่ปราศจากการคำนวณใดๆ เป็นหลักการที่เรียบง่าย มีอยู่ว่า แค่เดินขึ้นไปยังดาดฟ้าตึกพร้อมเชือกและบารอมิเตอร์ จากนั้นผูกบารอมิเตอร์เข้ากับเชือก แล้วหย่อนลงมาจากดาดฟ้าตึก เมื่อบารอมิเตอร์แตะพื้นก็ทำการวัดความยาวของเชือกที่ใช้ดิ่งไป ซึ่งแน่นอนมันก็คือความสูงของตึกนั่นเอง
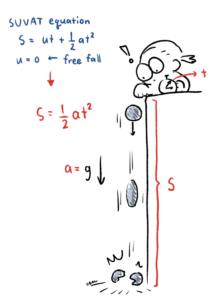
ถ้าอยากจะโชว์ความรู้ทางฟิสิกส์ซักหน่อยก็ลองมาดูวิธีที่ 2 คือ ปล่อยบารอมิเตอร์ลงจากดาดฟ้าตึก แล้วจับเวลาที่ใช้ตั้งแต่ปล่อยบารอมิเตอร์จนมันตกถึงพื้น แต่ต้องให้แน่ใจนะว่าวันนั้นไม่มีลมแรงจนเป็นอีกปัจจัยที่มีผลต่อการตกอย่างอิสระ
จากที่เรารู้กันว่าการตกแบบอิสระสามารถคำนวณได้ด้วยสูตรดังภาพประกอบวิธีที่ 2 ใช้ค่าความเร่งเนื่องจากแรงโน้มถ่วง g = 9.81 ms-2 เป็นความเร่ง a เมื่อแทน t หรือค่าเวลาที่จับได้ลงไป เราก็จะได้ S เป็นความสูงของตึกออกมา
หรือถ้าอยากได้วิธีที่ดูซับซ้อนกว่านั้นหน่อย กับเนื้อหาที่ลึกเข้าไปอีกบทหนึ่งของการเคลื่อนที่เชิงฟิสิกส์ ก็นี่เลยวิธีที่ 3 ผูกเชือกยาว L เข้ากับบารอมิเตอร์ แล้วแกว่งแบบเพนดูลัมอย่างง่ายที่พื้น และบนยอดตึก ทำการคำนวณค่าอัตราเร่ง เนื่องจากแรงโน้มถ่วงโดยใช้คาบที่วัดได้จากสองตำแหน่งแล้วแทนค่าในสูตร
เมื่อได้ค่า g บนพื้นและบนยอดตึก ก็นำมาหาผลต่างด้วยการแทนค่าเข้าในสูตรค่าอัตราเร่ง เนื่องจากแรงโน้มถ่วง ณ ระดับความสูง h จากผิวโลก
โดย R คือรัศมีของโลก และ g=9.81 ms-2 ก็จะได้ผลลัพท์เป็นผลต่างระดับความสูงที่พื้น และระดับความสูงที่ยอดตึก หรือก็คือส่วนสูงของตึกดังขั้นตอนคำนวณในภาพ (ซับซ้อน ใช่ไหมล่ะ )
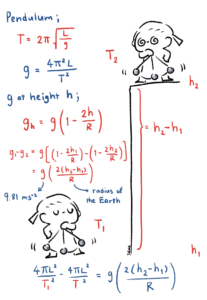
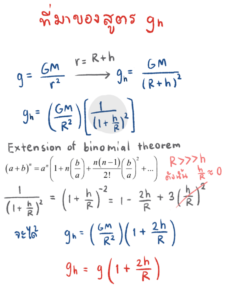
ใช้หลักการเคลื่อนที่แบบเพนดูลัมและการหาค่า g พร้อมพิสูจน์ที่มาของสูตร
คราวนี้ลองมาดูวิธีที่ 4 กันบ้าง โดยการประยุกต์ใช้ความรู้ทางคณิตศาสตร์ ในวันที่อากาศดี แสงแดดจ้า ก็หยิบเอาบารอมิเตอร์ตั้งฉากกับพื้นให้เกิดเงา แล้ววัดความยาวของเงาบารอมิเตอร์ ความสูงของบารอมิเตอร์ และความยาวเงาของตึก ก่อนคำนวณเทียบอัตราส่วนด้านคู่ที่สมนัยกัน ตามหลักสามเหลี่ยมคล้าย ก็จะได้ความสูงของตึกออกมา (สามเหลี่ยมจะคล้ายกันต่อเมื่อมีมุมเท่ากันสามคู่ ในกรณีนี้วัดพร้อมกัน มุมตกกระทบของแสงอาทิตย์ก็ย่อมเท่ากัน ส่วนมุมฉากกับมุมที่เหลืออยู่ก็เท่ากันไปตามๆ กัน)
ยัง…ยังไม่จบเท่านี้ ยังมีวิธีที่ 5 ถ้าเรามีเวลาเหลือเฟือและกล้ามเนื้อขาแข็งแรงสักหน่อยให้เดินหรือวิ่งขึ้นบันไดหนีไฟด้านนอกตึก แล้วใช้บารอมิเตอร์ทาบตามความสูงตึก และขีดเส้นตามผนังตึกไปเรื่อยๆ นับจำนวนครั้งไว้แล้วเอามาคูณกับความยาวของบารอมิเตอร์ เราก็จะได้ความสูงของตึกออกมา
จำนวนเท่าของความความยาวของบารอมิเตอร์
ท้ายที่สุดแล้วนักเรียนคนนี้ยังบอกอีกว่า วิธีที่ดีที่สุดก็คือวิธีที่ 6 ที่เขาบอกให้เดินถือบารอมิเตอร์นี้ไปยังชั้นใต้ดิน เคาะประตูห้องพักคนคุมตึก แล้วขอให้เขาบอกความสูงของตึก แลกกับบารอมิเตอร์ราคาแพงนี้ซะเลย นอกจากเร็วแล้วยังแม่นยำและน่าเชื่อถืออีกต่างหากไม่ต้องเสียเวลาคำนวณอะไรด้วย

วิธีที่ง่ายและประหยัดเวลาที่สุด
ช่างเป็นนักเรียนที่มีความคิดสร้างสรรค์อันล้นเหลือ น้อยคนนักที่จะคิดได้มากมายเช่นนี้ และแน่นอนว่าวิธีคำนวณผลต่างของความดันอากาศที่พื้นและบนยอดตึก จับเข้าสูตรหาความสูงตึกออกมา อย่างที่กล่าวไว้ในตอนต้นเป็นวิธีมาตรฐานที่เราๆ ก็สามารถทำได้หากผ่านการเรียนรู้ระดับมัธยมต้นตามหลักสูตร หากแต่การตอบคำถามเดียวกันนี้ สามารถทำได้หลายวิธีที่แตกต่างกันออกไป นอกเหนือจากวิธีที่มีอยู่แล้วโดยที่ยังคงเป้าหมายเดิมไว้ ดังที่นักเรียนคนนี้ได้นำเสนอ
ฉันคิดว่าหากผู้ออกข้อสอบเจอคำตอบที่หลุดกรอบออกนอกตำราเช่นนี้บ่อยๆ เขาคงเสียเวลาในการตรวจไม่น้อย แต่สำหรับฉันแล้ว ถ้าฉันเป็นครูแล้วเจอคำตอบที่แตกต่างกันออกไป ฉันคงสนุกกับการอ่านคำตอบ และยอมเสียเวลาทั้งวันที่จะนั่งฟังคำอธิบายจากนักเรียนสุดโต่งกลุ่มนี้
เรื่อง Angels on a pin ที่นำมาเล่าให้ฟังกันในวันนี้ ที่น่าสนใจอีกจุดคือ ชื่อของเรื่องสั้นนี้มีที่มาจากสำนวน “Angels on the head of the pin” ที่มาพร้อมคำถามที่ว่า “จงหาจำนวนของนางฟ้าที่ยืนอยู่บนหัวเข็มหมุด” หนึ่งใน reductio ad absurdum (การพิสูจน์ว่าคำกล่าวหนึ่งๆ เป็นไปไม่ได้ โดยใช้เหตุผลสุดโต่งและตรรกะวิบัติมาโต้แย้ง) คำกล่าวทางตรรกะพวกนี้ สร้างขึ้นเพื่อล้อเลียนลัทธิอัสมาจารย์ (scholasticism) หรือการเรียนการสอนวิธีคิดเชิงวิพากษ์ของนักวิชาการในมหาวิทยาลัย แสดงให้เห็นว่าวิธีแก้ปัญหานั้น ไม่ ต้องอิงตามหลักวิชาการเพียงอย่างเดียว ซึ่งก็อธิบายเรื่องราวที่ยกมานี้ได้เป็นอย่างดี ว่าการแก้ปัญหานั้นไม่จำเป็นต้องทำตามขั้นตอน และหลักการที่ปรากฏอยู่ในหลักสูตรตำราเรียนเสมอไป เพียงแต่ให้การหาคำตอบนั้นมีหลักของเหตุและผลที่เหมาะสมก็เพียงพอแล้ว
ฉันเห็นด้วยว่าในบางครั้ง หลักการตามตำราที่ได้เรียนรู้มา ก็กลายเป็นอุปสรรคชิ้นใหญ่ ที่บดบังการคิดแก้ปัญหาแบบพื้นฐานอย่างสร้างสรรค์ตามสัญชาตญาณของเรา บางทีการที่เราเรียนรู้วิธีแก้เฉพาะทางสำหรับปัญหาหนึ่งๆ ที่ผู้อื่นสร้างขึ้นมาให้ กลับทำให้เรามืดบอดในการพยายามหาคำตอบด้วยวิธีอื่น
ออกจะน่าเสียดายหากสุดท้ายทุกคนเลือกวิธีเดียวกัน ได้คะแนนเต็มเหมือนกัน ทั้งๆ ที่หากเราลองละทิ้งความรู้เดิมๆ ไปเสียบ้าง หรือมองในมุมกลับกัน บางทีเราอาจจะค้นพบหนทางใหม่ที่น่าสนุก และท้าทายกว่าแบบเดิมที่เป็นอยู่อีกมากมาย
ในการแก้ปัญหาวิทยาศาสตร์ ความรู้ทำให้เราแก้โจทย์ได้ทันทีโดยไม่ต้องคิดมาก แต่ขณะเดียวกันความไม่รู้ก็ก่อให้เกิดจินตนาการที่ทำให้เราคิดมากขึ้น ค้นคว้ามากขึ้น เกิดความคิดใหม่ๆ และค้นพบวิธีการใหม่ๆ ที่ไม่มีถูก ไม่มีผิด ท้ายที่สุดแล้วเราก็บรรลุผลลัพธ์ได้เหมือนเดิม เพิ่มเติมคือความสนุกและความเป็นเอกลักษณ์ ที่อาจนำไปสู่การสร้างสรรค์สิ่งประดิษฐ์ใหม่ขึ้นมาบนโลกก็เป็นได้ เพราะฉะนั้นอย่าได้เสียกำลังใจหากผลสอบออกมาไม่เป็นอย่างที่เราคาดหวัง
การที่เราคิดต่างกับคนอื่นไม่ใช่เรื่องผิดอะไร ขอเพียงคิดต่างแล้วสามารถอธิบายถึงเหตุผลที่มาที่ไปได้ เพียงเท่านี้ไม่ว่าปัญหาจะยากแค่ไหนก็จะสามารถแก้ไขได้ด้วยวิธีการอันสร้างสรรค์
แล้วเพื่อนๆ ล่ะ เลือกที่จะทำตามการท่องจำจากตำราการค้นพบของคนอื่น หรือจะเริ่มต้นทบทวนและจินตนาการเส้นทางใหม่ด้วยตนเอง
หากใครมีวิธีตอบโจทย์ข้อนี้ด้วยวิธีที่แตกต่างไปจากข้างต้น อย่าลืมเขียนมาเล่าให้กันฟังบ้างล่ะ !
ขอบคุณที่มาข้อมูลจาก:
เรื่องสั้น Angels on a Pin (101 Ways to Use a Barometer) by Alexander Calandra จากหนังสือพิมพ์ The Saturday Review ฉบับวันที่ 21 เดือนธันวาคม ปี ค.ศ. 1968
(ฉบับออนไลน์: https://www.unz.com/print/SaturdayRev-1968dec21-00060/)