เรื่องและภาพโดย ไอซี – วริศา ใจดี
ในวันแรกของชีวิตการเป็นนักศึกษามหาวิทยาลัย ฉันเองไม่ได้เตรียมใจไว้เลยว่า คาบแรกของการเรียนวิชาคณิตศาสตร์จะได้นั่งเล่นเกมและดูมายากลแสนสนุก ?! จนอดสงสัยไม่ได้ว่าฉันคงไม่ได้เข้าผิดห้องใช่มั้ยนี่ ?!
เมื่อพูดถึงมายากลและของเล่นแปลกๆ ที่ก้ำกึ่งระหว่างวิชาการกับงานประดิษฐ์ อย่างจิ๊กซอว์พิศวงที่ฉันเคยพูดถึงเมื่อสาระวิทย์ฉบับที่ 98 เดือนพฤษภาคม พ.ศ. 2564 และอื่นๆ อีกมากมายที่ล้วนดึงดูดให้ทั้งคนชอบวิทย์และศิลป์ร้องว้าวไปตามๆ กัน ทำให้ฉันนึกถึงคุณมาร์ติน การ์ดเนอร์ (Martin Gardner) ขึ้นมาทันที และในวันที่ 21 ตุลาคมที่จะถึงนี้ ก็เป็นวันครบรอบวันเกิดของคุณมาร์ตินซะด้วย เนื่องในโอกาสนี้ สาระวิทย์ในศิลป์ฉบับนี้จึงขอนำทุกคนเข้าสู่มิติใหม่แห่งการเรียนคณิตศาสตร์ผ่านของเล่น
คุณมาร์ตินเป็นนักคณิตศาสตร์และนักเขียนเชิงวิทยาศาสตร์ชาวอเมริกันชื่อดัง เขาเป็นคนแรกที่ได้รวบรวมเรื่องราวการอธิบายคณิตศาสตร์เชิงสร้างสรรค์ผ่านเกมกลสนุกๆ ตีพิมพ์ลงนิตยสาร Scientific American ให้เราได้อ่านกัน ถือเป็นผู้บุกเบิกวงการคณิตศาสตร์สานศิลป์คนสำคัญ ซึ่งหนึ่งในกลเกมแสนสนุกนั้นเป็นของเล่นสุดเจ๋งที่ชวนให้ขบคิด นั่นก็คือ เจ้าเฟล็กซากอน (Flexagon) ของเล่นที่มีความลับซ่อนอยู่มากมาย เจ้าของเล่นรูปหกเหลี่ยมแบนๆ นี้ สามารถเปิดไปมาได้ไม่มีที่สิ้นสุด เล่นได้ไม่มีเบื่อ ที่สำคัญมันทำเองได้ง่ายๆ จากกระดาษ ไม่ต้องหาซื้ออุปกรณ์ให้เสียเงิน และไม่ต้องใส่แบตเตอรี่ด้วยละ ! น่าสนใจใช่ไหม อ่านจบฉบับนี้รับรองว่าทุกคนสามารถทำของเล่นเจ๋งๆ ด้วยตัวเอง เอาไปอวดเพื่อนๆ กันได้อย่างแน่นอน
เจ้าเฟล็กซากอนมีที่มาที่น่ามหัศจรรย์ยิ่งกว่ากลไกที่ลึกลับ โดยย้อนไปในปี พ.ศ. 2482 การค้นพบของเล่นสุดน่าทึ่งนี้ มีต้นเหตุมาจากการที่ขนาดของแผ่นกระดาษที่ผลิตใช้กันในสหรัฐอเมริกามีขนาดแตกต่างไปจากขนาดของแฟ้มเก็บกระดาษที่ผลิตจากประเทศอังกฤษ
ดังนั้นเมื่อพยายามจะใส่กระดาษเหล่านี้ลงไปในแฟ้ม ก็จะทำให้มีแถบกระดาษส่วนหนึ่งโผล่ยื่นเลยแฟ้มออกมา และเจ้าของแฟ้มที่ประสบกับปัญหาความไม่พอดีนั้น คือคุณอาร์เทอร์ เอช. สโตน (Arthur H. Stone) นักคณิตศาสตร์ชาวอังกฤษ ขณะที่เขายังเป็นนักศึกษาอยู่ที่มหาลัยพรินซ์ตัน ด้วยความเนี้ยบ คุณสโตนก็เลยตัดสินใจตัดแถบกระดาษส่วนเกินออกมา และในระหว่างที่นั่งเบื่อๆ เขาก็เริ่มพับแถบกระดาษเหล่านั้นเล่นเป็นรูปแบบต่างๆ กัน พับไปพับมาดันออกมาได้รูปหกเหลี่ยมด้านเท่าที่พอจับจีบให้ถูกมุมมันก็จะเปิดออกมาเป็นหน้าใหม่ได้ทุกครั้ง มันบิดได้หลายรูปแบบ แถมมีลักษณะเป็นทรงหกเหลี่ยม เขาเลยตั้งชื่อมันว่า hexaflexagon ซะเลย ซึ่งคำว่า hexa แปลว่าหก ขยายคำว่า flexagon ที่เกิดจากการผสมคำว่า flex หรือบิด กับคำว่า polygon ตามรูปลักษณ์ของมันที่เป็นรูปหลายเหลี่ยมที่พับขึ้นจากแถบกระดาษ ที่สำคัญก็คือ มันสามารถเปลี่ยนหน้าได้เมื่อพับให้โค้งงอขึ้น แล้วเปิดออกตามทิศทางต่างๆ ดังภาพประกอบที่ 1

ภาพประกอบที่ 1 แสดงการบิดเจ้าเฮกซะเฟล็กซากอน
คุณสโตนตื่นเต้นกับการค้นพบครั้งนี้มาก รีบนำไปอวดเพื่อนๆ และคุณครูของเขา หนึ่งในนั้นเป็นคนที่ถ้าเอ่ยชื่อถึงทุกคนคงจะคุ้นหูกันดี เขาคือ คุณริชาร์ด พี. ไฟยน์แมน (Richard P. Feynman) นักฟิสิกส์ทฤษฎีชื่อดัง ผู้นำเสนอวิธีการเข้าใจควอนตัมฟิสิกส์ในแบบใหม่ ซึ่งในตอนนั้นคุณไฟยน์แมนเป็นเพียงนักศึกษาสาขาฟิสิกส์ที่สนใจการเล่นพับกระดาษเท่านั้นเอง แต่แล้วด้วยความร่วมมือของเพื่อนๆ สมาคมเฟล็กซากอน (Flexagon committee) จึงก่อตั้งขึ้น พวกเขาได้ทำการศึกษาลงลึกไปถึงกลไกของ Flexagon ทั้งลำดับการเปลี่ยนหน้า เงื่อนไขต่างๆ จนได้เป็นทฤษฎีและแผนผังที่โยงเรื่องราวการเล่นอันแสนสนุกนี้ไปสู่เนื้อหาวิชาการได้อย่างไม่น่าเชื่อ อ่านมาถึงตรงนี้ ทุกคนคงอยากจะเล่นเจ้าของเล่นอันแสนมหัศจรรย์ชิ้นนี้แล้วใช่ไหม เอาละ ! ฉันขอชวนเพื่อนๆ มาลงมือทำของเล่นชิ้นนี้กันก่อนที่จะเข้าสู่เนื้อหาทางวิชาการ
Hexaflexagon ประกอบขึ้นมาจากกระดาษแถบยาวที่แบ่งเป็นสามเหลี่ยมด้านเท่าเรียงกลับด้านสลับกันไปมา ก่อนอื่นเราจึงต้องหาแถบกระดาษที่มีความยาวสักหน่อย ซึ่งขนาดชิ้นของเจ้าของเล่นหกเหลี่ยมที่ได้นั้นจะขึ้นอยู่กับความกว้างของแถบกระดาษ ดังนั้นเราจึงปรับได้ตามใจชอบ ถ้าต้องการสามเหลี่ยมความยาวด้านละ x หน่วย ตามทฤษฎีบทพีทาโกรัส ความกว้างของแถบกระดาษ (ความสูงของสามเหลี่ยม) ก็ควรจะเป็น หน่วย ดังภาพประกอบที่ 2
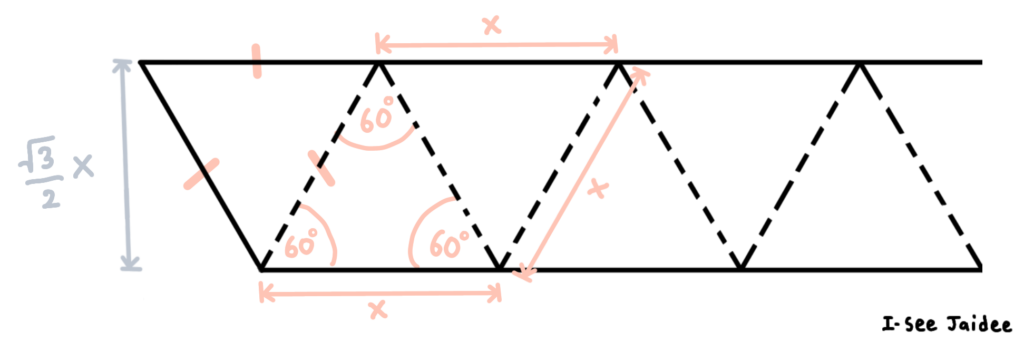
ภาพประกอบที่ 2 แสดงขนาดของสามเหลี่ยมด้านเท่าที่สัมพันธ์กับความกว้าง และความยาวของแถบกระดาษในการทำเฮกซะเฟล็กซากอน
จะต้องใช้สามเหลี่ยมกี่รูปนั้นก็ขึ้นอยู่กับว่าเราอยากให้เฟล็กซากอนเปิดได้กี่หน้า ซึ่งที่เราจะมาทำกันในวันนี้มีสองแบบด้วยกัน คือ ไตรเฮกซะเฟล็กซากอน (trihexaflexagon) และ เฮกซะเฮกซะเฟล็กซากอน (hexahexaflexagon) แค่อ่านชื่อก็ลิ้นพันกันแล้ว ไปดูกันดีกว่าว่ามันต่างกันอย่างไร
แบบแรก ไตรเฮกซะเฟล็กซากอน เปิดได้ 3 หน้า ภาพคลี่ของมันเป็นแถบสามเหลี่ยมด้านเท่าจำนวน 10 รูป หลังได้แถบกระดาษคุณสมบัติตามข้างต้นแล้ว ดูขั้นตอนการทำไตรเฮกซะเฟล็กซากอนทีละขั้นตามภาพประกอบที่ 3 กันได้เลย
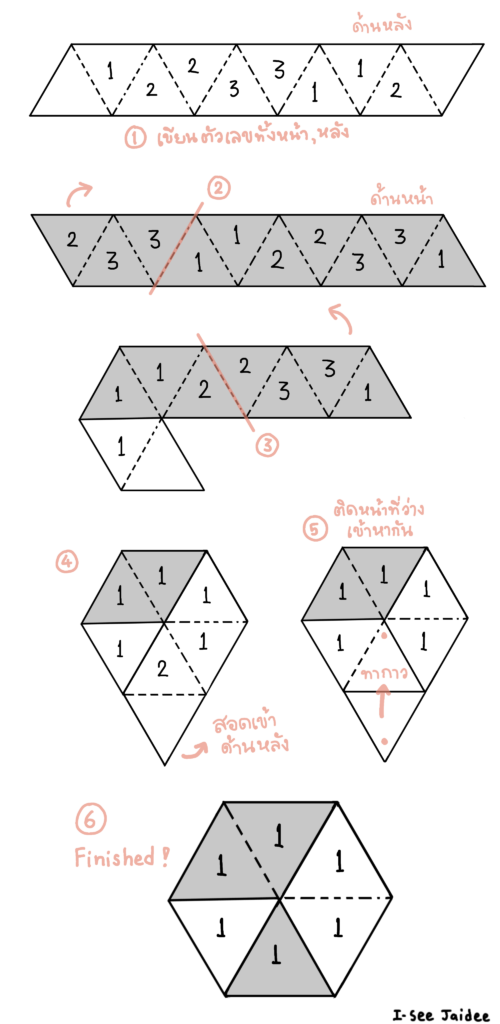
ภาพประกอบที่ 3 ขั้นตอนการทำไตรเฮกซะเฟล็กซากอน
– แบบที่สอง เฮกซะเฮกซะเฟล็กซากอน เปิดได้ 6 หน้า ครั้งนี้เราต้องการแถบสามเหลี่ยมด้านเท่าทั้งหมด 19 รูปด้วยกัน ซึ่งจะซับซ้อนมากกว่าแบบแรกที่เปิดได้เพียง 3 หน้า มาลองทำตามทีละขั้นดังภาพประกอบที่ 4 กันเลย
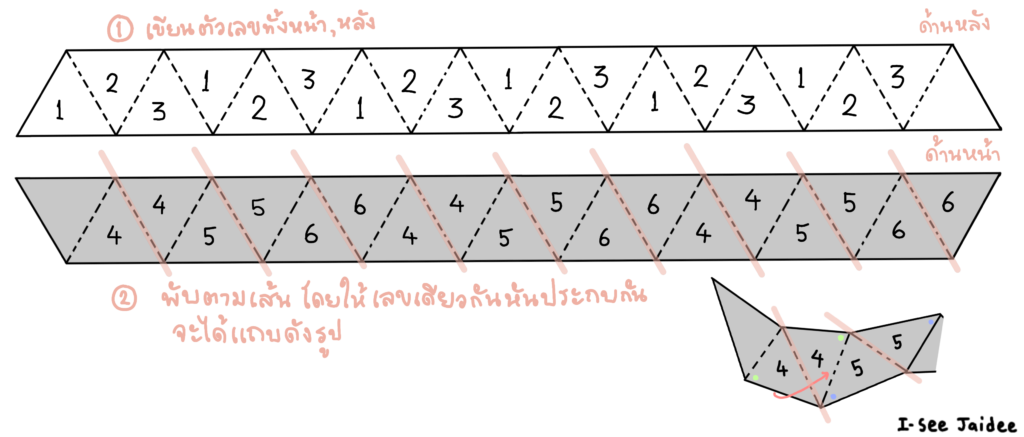
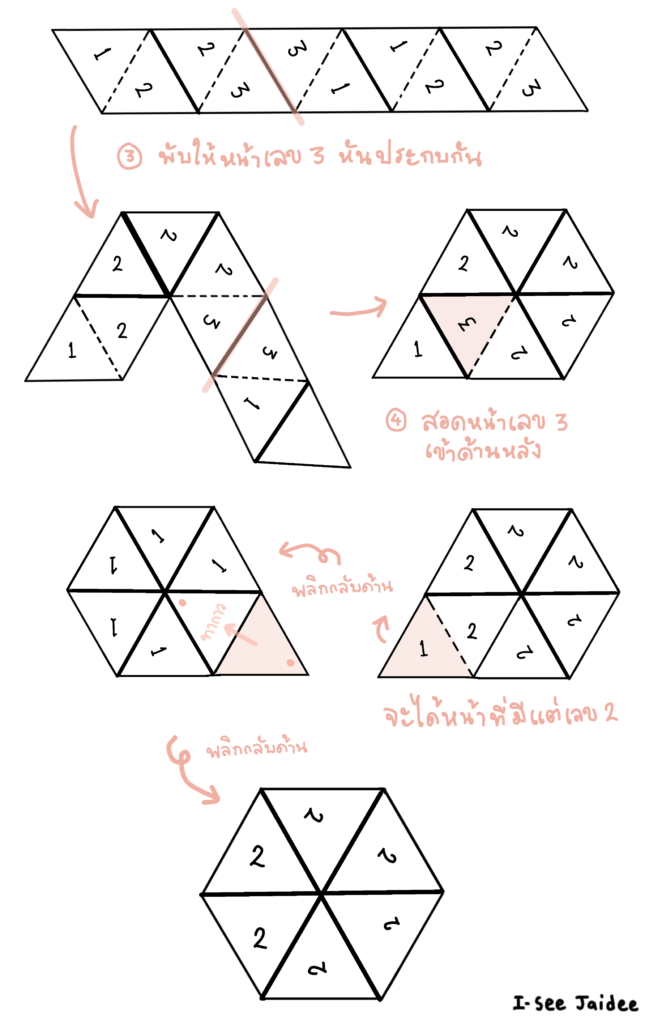
ภาพประกอบที่ 4 ขั้นตอนการทำเฮกซะเฮกซะเฟล็กซากอน เมื่อทำเสร็จแล้วลองเล่นดู เพื่อนๆ สังเกตเห็นอะไรแปลกๆ รึเปล่านะ ?
ในแบบแรกดูจะไม่มีปัญหาอะไร หน้าทั้งสามปรากฏขึ้นมาให้เห็นตามลำดับตามที่เราคาดไว้ แถมยังเรียงเหมือนเดิมไม่สลับไปมา ไม่เชื่อก็ลองวาดรูปลงไปดูเลย รับรองเปิดกี่ทีก็ยังได้รูปสวยเหมือนเดิมถึงสามรูปที่แตกต่างกัน
แต่ปัญหาอยู่ที่แบบที่สอง ถ้าได้ลองเล่นแบบที่สองดูแล้ว เราจะพบว่าบางทีเราก็เปิดเจอไม่ครบหน้า หรือบางหน้าเปิดได้สองทางบ้าง ทางเดียวบ้าง แล้วมันมีรูปแบบตายตัวหรือเปล่านะ ?
ฉันได้ทดลองพลิกเล่นและจดลำดับแบบรูปการเปลี่ยนหน้าออกมา ซึ่งกรณีแรก เริ่มที่หน้าเลข 2 โดยยึดขอบที่ไฮไลต์สีฟ้าดังรูป เมื่อเปิดออกมาก็จะพบกับเลข 5 ซึ่งสามารถเปิดได้ทางเดียวออกมาเป็นเลข 1 ซึ่งเปิดได้ทางเดียวเช่นกันวนกลับไปเป็นเลข 2 ถ้าเราเปิดแบบนี้ต่อไปเรื่อยๆ ก็จะวกอยู่แค่ 3 หน้านี้ ได้แก่ 2>5>1 (ภาพประกอบที่ 5) ซะงั้น ?! แล้วตัวเลขหน้าอื่นๆ ที่เราเขียนไว้ล่ะ ?
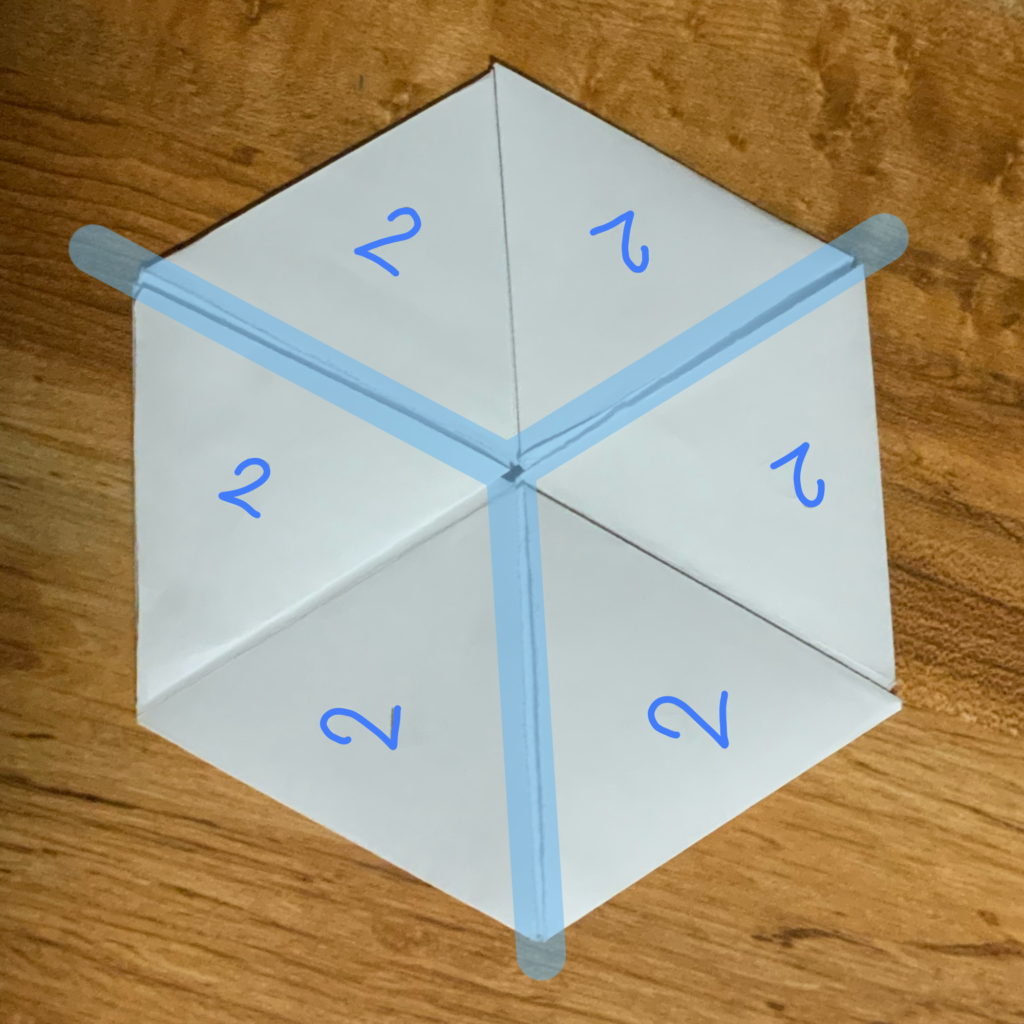


ภาพประกอบที่ 5 ลำดับการเปลี่ยนหน้าของเฮกซะเฮกซะเฟล็กซากอนแบบ 2>5>1
อย่าเพิ่งตกใจไป นี่ไม่ใช่ของเล่นลวงโลกแต่อย่างใด ลองเปิดกลับไปที่หน้าเลข 2 อีกครั้ง เราจะพบว่า มันสามารถเปิดได้ถึง 2 ทางด้วยกัน ถ้าเราลองเปิดทางที่ต่างไปจากรอบแรกซะก็จะเจอตัวเลขที่ซ่อนอยู่ นั่นก็คือ… เลข 3 จากนั้นฉันก็เปิดต่อไปแบบเพลินๆ ตามครั้งแรก เลข 4 ก็ปรากฏตัวออกมา แต่ทว่าดูเหมือนเราจะเจอทางตันเข้าให้ เพราะหน้าเลข 4 นั้นมีทางเดียวให้เปิดออก และก็เป็นไปตามที่คาดคิดไว้ เราวนกลับมาที่เลข 2 อีกแล้ว ทำให้ในรอบนี้เราได้ลำดับออกมาคือ 2>3>4 (ภาพประกอบที่ 6)



ภาพประกอบที่ 6 ลำดับการเปลี่ยนหน้าของเฮกซะเฮกซะเฟล็กซากอนแบบ 2>3>4
ลองเปิดสองแบบก็แล้ว เจอชุดตัวเลขใหม่ก็แล้ว แต่เหตุไฉนไม่มีเลข 6…เลข 6 ของเราไปซ่อนตัวอยู่ที่ไหนกันนะ ? ฉันอยากให้ทุกคนได้ลองทำเฟล็กซากอนทั้งสองแบบมาลองเปิดเล่นกันดูก่อนที่ฉันจะอธิบายว่าเลข 6 นั้นซ่อนตัวอยู่ที่ไหนให้ทุกคนได้รู้ในฉบับหน้า แต่หากใครหาเลข 6 เจอ ถ่ายรูปส่งมาที่เพจนิตยสารสาระวิทย์ได้นะคะ มาเล่าให้ฟังกันด้วยว่าหาเจอได้ยังไง ?! เพจสาระวิทย์มีรางวัลมอบให้ด้วยนะ ฉบับนี้ขอลาไปก่อน สุขสันต์เดือนแห่งเฟล็กซากอน ขอให้เล่นให้สนุกนะ !
ขอบคุณข้อมูลจาก:
- หนังสือ Hexaflexagons and Other Mathematical Diversions: The First ‘Scientific American’ Book of Puzzles and Games โดยคุณ Martin Gardner
- Vihart – ช่องยูทูบของคุณ Vi Hart นักคณิตศาสตร์ชาวอเมริกัน











